The challenges of climate change cannot be fully captured if they are reduced solely to sector-, region- or technology-specific aspects. Even a strict distinction between measures to mitigate climate change and adaptation measures does not meet these challenges. An integrative approach, which does not separate adaptation and mitigation, is adopted, for instance, in the discussion about sustainable cities [1]. Sustainable cities involve planning urban development measures that take into account their social, economic, and ecological consequences. In addition to the goal of reducing the climate impact of cities (for example, by improving the efficiency of buildings or expanding local public transport), sustainable cities are also about enabling people in metropolitan areas to adapt to expected rising temperatures (for example, through drainage and irrigation measures or be greening buildings). Such an integrative approach can also be transferred to the planning of infrastructure measures in the areas of energy supply, drinking water and protection against extreme weather events. For example, water storage infrastructures simultaneously touch on aspects of energy storage, the provision of drinking water or other types of ecosystem services.
However, the planning of projects that are equipped with such a multi-dimensional range of system services faces particular challenges. This paper presents such a project from a low mountain region in Germany.
The interdisciplinary nature of the project stems from the fact that several, sometimes very different, research areas are addressed simultaneously. Firstly, questions arise about the regional effects of climate change in low mountain regions and the adjacent lowlands; these effects ask for the design of measures for regional adaptation. Secondly, since adaptation measures with respect to water management particularly look at the regional water management infrastructure, it makes sense to also consider the embedded possibilities of energy storage when planning such projects. Thirdly, the question arises as to how the advantages and disadvantages, seen in the different ecological, water management and energy management dimensions, can be weighed up when evaluating and deciding on alternative projects.
The literature on regional impacts of climate change is very diverse. Climate problems in coastal regions, for example, differ significantly from the problems in lowlands and mountain regions. Basically, mountain regions reduce the variability of flows in the adjacent lowlands as they provide a temporal redistribution of precipitation in winter to runoff in spring and summer. Mountain water resources are essential for a couple of services, such as irrigation or municipal and industrial water supply [2]. Adapting to these problems involves public and private planning decisions and linking estimated climate impacts with vulnerability research [3]. As the effects of climate-related temperature increases vary with the altitude of the respective region, McDowell et al. [4] develop a typology of climate change effects in glaciated mountain systems. They highlight – for instance – the sensitivity of mountain systems to changes in temperature and map climate-related changes onto diverse social settings, reflecting the link between geographic factors and socio-political histories. Other papers, such as Rüegg et al. [5] investigate the link between mountain forests and hydrological regimes, especially with respect to protection services against floods and the interaction between forests and runoffs. Vij et al. [6] present a literature overview of papers on climate impacts for biophysical systems in European mountain regions (such as the reduction in forest carbon, changes in tree heights or vegetation patterns) and investigate how these changes affect human systems in the field of water availability, tourism or agricultural production. Their analysis suggests that climate vulnerability is relatively high in certain European regions (especially in eastern and southeastern Europe) with only limited adaptive capacities. As mountain regions represent a special type of a social-ecological system, they call for a context-specific governance arrangement in European Mountain regions. However, the need to develop sound adaption strategies for mountain ecosystems is limited by data gaps and uncertainties [7]. Eckhardt and Ulbrich [8] investigated the impacts of climate change on groundwater and streamflow in European low mountain regions. They show that the proportion of winter precipitation falling as snow will decline, thereby reducing spring snowmelt peak in spring and increasing the flood risk in winter. In summer the groundwater recharge and streamflow might be reduced by 50%. Modelling a representative catchment within Germany's low mountain range, Grosser and Schmalz [9] expect extending drought periods (despite wetter winters) and estimate a 68% increase in dry period duration due to intensified water stress in summer and autumn.
The strand of literature that deals with linking issues of energy system transformation with other issues of ecosystem service provision is less extensive. Water reservoirs and water storage of low mountain regions simultaneously can be used for electrical storage and as measures to adapt to the regional effects of climate change.
The technologies for the storage of electrical energy can be classed according to Sauer et al. [10]:
Electrical (Super-Capacitor)
Mechanical (Pumped Hydro Power, Compressed Air Energy Storage System, Flywheel)
Thermal (Thermoelectric Storage)
Chemical (Batteries, Hydrogen Storage, Natural Gas Storage).
In the following, the focus will be on pumped hydropower because it is suitable for storing rather large amounts of energy, which can be made available quickly and at a lower cost than many alternatives [10], [11]. Additionally, many of the usual caveats against pumped hydropower, such as geographical restrictions due to the requirement of two new basins, do not apply here [12]. Soha et al. [13] investigate the surface and underground infrastructure of the former mining industry and state that low mountain water reservoirs from mining involve a high potential when used as new elements of a flexible and sustainable energy system. However, they also identified a research gap to examine the possibility of pumped hydroelectric energy storage, which has to be filled with adaptable geographical information systems. Similarly, Alvarez et al. [14] and Döhren and Haase [15] suggest the use of underground pumped hydroelectric storage of mine water. Such a hybrid hydro-wind system could become an efficient and flexible alternative to dealing with intermittent renewable energy sources. Gurung et al. [16] expect that hydropower systems in the Alps can serve as European "water towers" and provide energy storage when extending hydropower production. However, they also state that this remains controversial because of environmental drawbacks.
Another part of the literature deals with the connection between these environmental drawbacks and the planning of such infrastructure projects. Adaptation measures such as raising dams or building new dams not only require long-term investments but also represent deep interventions in the environment and nature, and they often face large local resistance. Installing a hydro-power station – for instance – can modify the river course and affect the integrity of the environment and its ability to spend other ecosystem services. The commitment of financial resources and the consequences of landscape interventions must be weighed against the benefits of the expected ecosystem services. Stremke and Dobelsteen [17] assumed that quantifying the impact of energy transition on landscape quality was of growing importance. They developed some practical guidelines for planning such sustainable energy landscape projects. They presented a set of case studies and practical applications, allowing stakeholders to participate actively during the planning phase. In order to achieve the necessary social acceptance, an evaluation framework must be developed reflecting the multidimensionality of the problems. Such an evaluation framework must also be able to support the social process of involving local stakeholders in the decision on the implementation of such measures. Papers in this field of research, such as Picchi et al.[18] or Kienast et al. [19], agree that further research is needed on how to deal with these trade-offs. One problem with weighting and balancing these trade-offs is that different stakeholder groups associate different interests and perspectives with the respective measures. Local communities, for instance, are highly focused on the visual impacts of infrastructure measures on the landscape, and farmers might be more interested in the consequences on food production.
In contrast, environmental organisations are more concerned about the consequences for the integrity of larger ecosystems. Galler et al. [20] discuss the advantages and disadvantages of economic evaluation methods to deal with such kind of trade-offs. The decisive advantage of economic evaluation methods is that they not only allow different target dimensions to be weighted but also that these target dimensions can be offset against each other when a uniform, commensurable value standard is applied. However, they state that economic valuation should not replace specific physical or biological assessments of ecosystem services. An economic analysis could – for example – suggest preferring drinking water treatment instead of preventing pollutants from infiltrating into groundwater. The argument of cost-efficiency of restoration should not offset the high value that society attaches to clean groundwater protection as stipulated in the law or certain standards. However, they see room for economic valuation methods as tools for decision-making and prioritising alternative measures when a clear structure of objectives obtained from legislation or other standards is missing.
This paper discusses the project labelled "Energy and water storage in the Harz mountain range". This project was funded within the innovation guideline by universities and research institutions in the field of innovation networks specialising in energy management in the period July 2019 to June 2022 with the European Regional Development Fund (ERDF) [12]. In addition to the changes in the electrical energy system with increased integration of renewable energies, the regional background to the project was the effects of climate change in the Harz Mountains in northern Germany, as they occurred in 2017 and 2018. First, the region was hit by a 1000-year flood. Shortly after that, a long-lasting drought followed with record minus values for precipitation. With an increasing proportion of fluctuating, regenerative feed-ins into the power grid, energy storage systems make substantial contributions to a functioning energy system by balancing the provision and use of energy. These technologies play a key role in grid stabilisation, particularly to balance the residual load. Storage capacities in northern Germany are particularly important in combination with wind energy, which also largely feeds into the grid in northern Germany, in order to make better use of line capacities and to provide electrical system services such as instantaneous reserves on site.
In a 2014 study, Babrowski et al. [21] stated that different types of storage systems can be used to prevent congestion in the German grid or to store surplus production from renewable sources. They also developed economic criteria for investing in storage capacities. In a similar study of electricity markets in Germany, Paulus and Borggrefe [22] investigated the possibility of integrating demand-side-management in energy-intensive industries with supply-side measures, such as expanding storage capacities.
In addition, large-scale pumped storage plants represent a technologically mature solution for the provision of such stabilising system services [10]. However, new potential does not appear to be realisable, primarily due to the significant interventions in nature and the associated problems of societal acceptance among the population, but also due to the lack of profitability under the current energy industry framework. It was shown that the long-term profitability of these systems is not given if they are marketed solely in an energy-only market. Nevertheless, the technology offers the potential to generate additional contribution margins in other areas (e.g. provision of system services) and to create additional economic benefits (e.g. integration into flood protection). Against this background, the project involved an innovative coupling and systemic consideration of energy and water management aspects. Since the Harz Mountains are hydrologically to be regarded as a large water surplus area and climate change projections indicate an increase in the mean annual water supply there in the future, such an integrative approach seems imperative (for a more comprehensive overview of the ERDF project, please refer to its final report [12]).
From an economic and social science point of view, the question arises as to how these different, partly complementary, but partly also opposing project dimensions can be integrated and prepared in a decision-oriented manner. Of course, it was not the task of the project to make such a decision, to simulate it, or even to prepare it. The innovative approach of the project is rather to show, in an integrated approach, how different system services in three fields – flood protection and low water elevation, protection of drinking water resources, and large-scale energy storage – can be used to generate and evaluate investment alternatives at different locations. In a decision-oriented assessment, of course, in addition to the different coupled system services, their monetary costs (from the investment and operation of the systems) and the consumption of environmental resources (e.g. due to interference with flora and fauna) must also be considered. The project focuses on two aspects in the foreground: How can alternatives be generated that are able to serve such a benefit profile? And how do we evaluate and prioritise these alternatives? The first step involves the generation and description of possible project alternatives and locations. Due to geological factors (such as river courses) and existing water storage capacities, such technically feasible project alternatives were generated at several locations in the Upper Harz, from which simultaneous, positive target contributions to all the target as mentioned above dimensions emanate.
With regard to the development of pumped storage, the study region is characterised, for example, by a low mountain range made of load-bearing rock and mines that are no longer used so that the large difference in height between the deep shaft and the upper reservoir, which is relevant for pumped storage operation, can be used. The development of older mines, while costly, avoids some of the usual environmental or acceptance issues otherwise associated with such infrastructure projects. In the second step, i.e., when comparing and evaluating these alternatives, the question arises as to how the benefits generated in the various target dimensions in the form of energy storage and ecosystem services can be determined, weighted and compared with each other. In addition, these target contributions must be compared with the necessary costs (investment costs and costs of ongoing operation) and the associated interventions in the landscape and natural resources (loss of flora and fauna, the intensity of the intervention in the landscape, and other factors).
The paper is organised as follows: In the next chapter, the theory and methodology of the AHP approach are derived. The alternatives that will be assessed within this framework are also presented in this methods section. The data collection procedure and the main results are presented and explained in the subsequent section. The insights gained are critically reflected in relation to the assumptions made and discussed in the context of the AHP literature. The paper concludes with some substantive and methodological considerations regarding its main results and the possibilities of applying the AHP approach to comparable decision-making problems.
The goal formulated in the project application calls for an economic evaluation of options for action as a decision-making aid when planning integrated measures for the system services of flood protection, low water level increase, drinking water supply and energy production or storage. This goal requires an evaluation of the options across partially conflicting dimensions. In decision-theoretic literature, decision-making procedures that are intended to meet the criterion of rationality for multi-dimensional goals are referred to as multicriteria, confer Vučijak et al.[23], and Karatzas et al. [24]. The solution of multicriteria problems implies the following elements both in individual decisions and – as in the project "Energy and water storage in the Harz mountain range" – in group or collective decisions:
Multiple goals: Multiple goals or properties of the alternatives must be considered simultaneously. These goals need to be clearly articulated before the decision-making process begins and then taken for granted. The available alternatives are later to be evaluated against these goals in order to make a rational decision. It must, therefore, be possible to describe the available alternatives independently of one another on the basis of their characteristics in the relevant target dimensions. Here, focusing on one main goal and ignoring other goals should be avoided.
Conflicting goals: In the forms of the alternatives in the various goal dimensions, the degrees of goal achievement of some criteria are negatively linked: the improvement in one criterion often leads to a deterioration in at least one other so that the advantages and disadvantages of different goals have to be weighed against each other. In addition, the degree of goal attainment in one goal dimension can often only be poorly compared with the degree of goal attainment in other dimensions.
Determination of the solution to the decision problem: From the available alternatives, the one that appears most favourable should be selected when all objectives are taken into account simultaneously.
Usually, multicriteria problem-solving mechanisms in decision theory distinguish two classes of approaches. The first class consists of so-called MODM methods (Multi-Objective Decision Making) [25]. Decision problems are described as mathematical optimisation problems. Here, it is assumed that optimal alternatives for action can be generated with the help of a target function and appropriately formulated constraints that restrict the solution space to permissible solutions. The explicit specification of a target function enables the formalisation of trade-offs between the individual criteria. Within the permissible multi-dimensional solution space, an optimal alternative is identified by means of mathematical optimisation. Since the alternatives in the project were not to be identified endogenously on the basis of logical or mathematical considerations on the "green field" but from the status quo of existing location and infrastructure factors, the AHP is an application of MADM (Multi-Attributive Decision Making) methods, where a concrete set of permissible solutions is already given [25]. First, the criteria chosen by the decision maker are compared to determine their relative weights. Alternatives are compared with one another based on their attributes. The advantage of this method is that target dimensions can also be represented in a non-quantitative form. It is assumed that the decision maker is able to make a relational preference statement when comparing two alternatives within a certain dimension. In MADM procedures, the search for the best alternative is in the foreground – or, in the best case, even the complete ranking of all solutions [25], [26].
When applying an economic welfare analysis, or at least a cost-benefit analysis, the problem of value determination arises. Although market data are available to determine the value of electrical energy generation from pumped storage facilities or the production of drinking water, it is not easy to offset the values resulting from the commercial operation of such a system against the value of ecosystem services. These are firstly difficult to quantify due to their multidimensionality, and secondly (e.g., in the area of flood protection) are assigned to the non-market area of public services and non-excludable public goods. However, the simultaneous generation and consideration of ecological and energy system services represent a significant innovation of this infrastructure project. The project also refrained from using simple scoring models in order to evaluate expected benefits, which also would allow for including non-monetary target dimensions. When applying a scoring model, decision-makers are given the task of explicitly weighing the goals and then evaluating the alternatives within each dimension. The result of this multi-attribute evaluation of an alternative is a one-dimensional utility value. Although this rather pragmatic approach to utility analysis is similar as compared to the Analytical Hierarchy Process (AHP), the AHP model is a mathematically more sophisticated method based on matrix operations, in which the information about the weighting of the goal dimensions and the evaluation of the alternatives within these goal dimensions is not collected in absolute terms, but is obtained through a series of pairwise comparisons. The term "hierarchical" implies that the target dimensions are broken down into different hierarchical levels. In the 1970s, the mathematician Saaty presented the Analytical Hierarchy Process (AHP) as a multi-attribute decision-making process as a further development of utility analysis [26], [27]. This further development referred above all to the fact that the weights and the transformation of characteristic values are no longer requested directly from the decision-maker (as in the utility value analysis) but are determined from pairwise comparisons. This method is used in applied decision research. It can be used for group decisions in the context of expert surveys, particularly in the areas of management, product development or healthcare, confer Hummel et al. [28] and Vaidya and Kumar [29].
The AHP methodology is also used in the construction industry to evaluate infrastructure projects. For example, Belay et al. [30] show how different, sometimes conflicting goals and interests of stakeholders can be balanced in an AHP process to determine a target system for construction projects. In the area of water management systems planning, the AHP model is often used to support decision-making. For example, using expert interviews whose data are transferred to the AHP model, Xu et al. [31] develop findings on how an optimal mix of green and grey infrastructure elements can be determined, taking into account local factors (such as the flood risk of a region). Similarly, Sun et al. [32] apply the AHP methodology to the evaluation of different agricultural water management systems in floodplain regions. Motiee et al. [33] show how the AHP methodology can be used to develop a system of technical, ecological and economic criteria for evaluating large-scale water transfer systems. Thungngern et al. [34] provide an overview of the various applications of the AHP method to the planning of water management systems. They particularly emphasise the advantages of this method in taking into account and integrating different economic, ecological and social evaluation criteria. The AHP method is also used in a variety of ways when planning energy infrastructure projects. For example, Garbuzova-Schlifter and Madlener [35] used the AHP method to identify, weight and evaluate specific energy project risks. Lee et al[36] used an AHP approach to determine a competitiveness profile of different providers and technologies for hydropower generation. An example, showing how the AHP method can be used as a policy decision support system when planning to transform entire energy systems, was provided by Toossi et al. [37]. However, until today no consideration of coupled water and energy infrastructure measures has been presented in the literature in this area.
In terms of decision theory, the procedure is based on a series of rationality axioms, which are needed to assume that evaluation can be carried out using pair comparisons. With the AHP, the overall goal is “resolved" into target dimensions in order to evaluate the projects that are available and pending with regard to these dimensions. This procedure can be described using the following process steps:
Step 1: The overall goal is broken down into sub-goals (this goal structure is to be taken as given since it was already defined in the project application).
Step 2: A pairwise comparison is made between the targets. From this, the weightings of the target dimensions are derived. The question posed to the decision-maker is: How important is target dimension A compared to target dimension B for the overall goal?
Step 3: Within every target dimension, comparisons are made between the alternatives. The question asked here is: How does alternative A perform in this target dimension compared to alternative B? All pairs of alternatives are compared within a target dimension. Then, all target dimensions are processed in this way.
Step 4: The information obtained in the course of steps 2 and 3 is linked. Since the decision was made by a group of decision-makers (project team and practice advisory board), this information must also be aggregated.
Step 5: The consistency of the information obtained is checked, in particular with regard to heterogeneity (consensus in the group) and sensitivity analyses, for example, with regard to changes in the weighting of target dimensions.
One of the cornerstones of this procedure is that a target system is developed, which is then to be used for the evaluation of a set of sufficiently defined and independent alternatives. The advantage of this method is that the weighting of the individual target dimensions does not have to be specified exogenously but is determined by the individual decision-makers or the members of a decision-making body in the course of their preference statements. The structure of the target system shown in Figure 1 (but not the respective weighting) results in principle from the original ERDF project application:
Target system
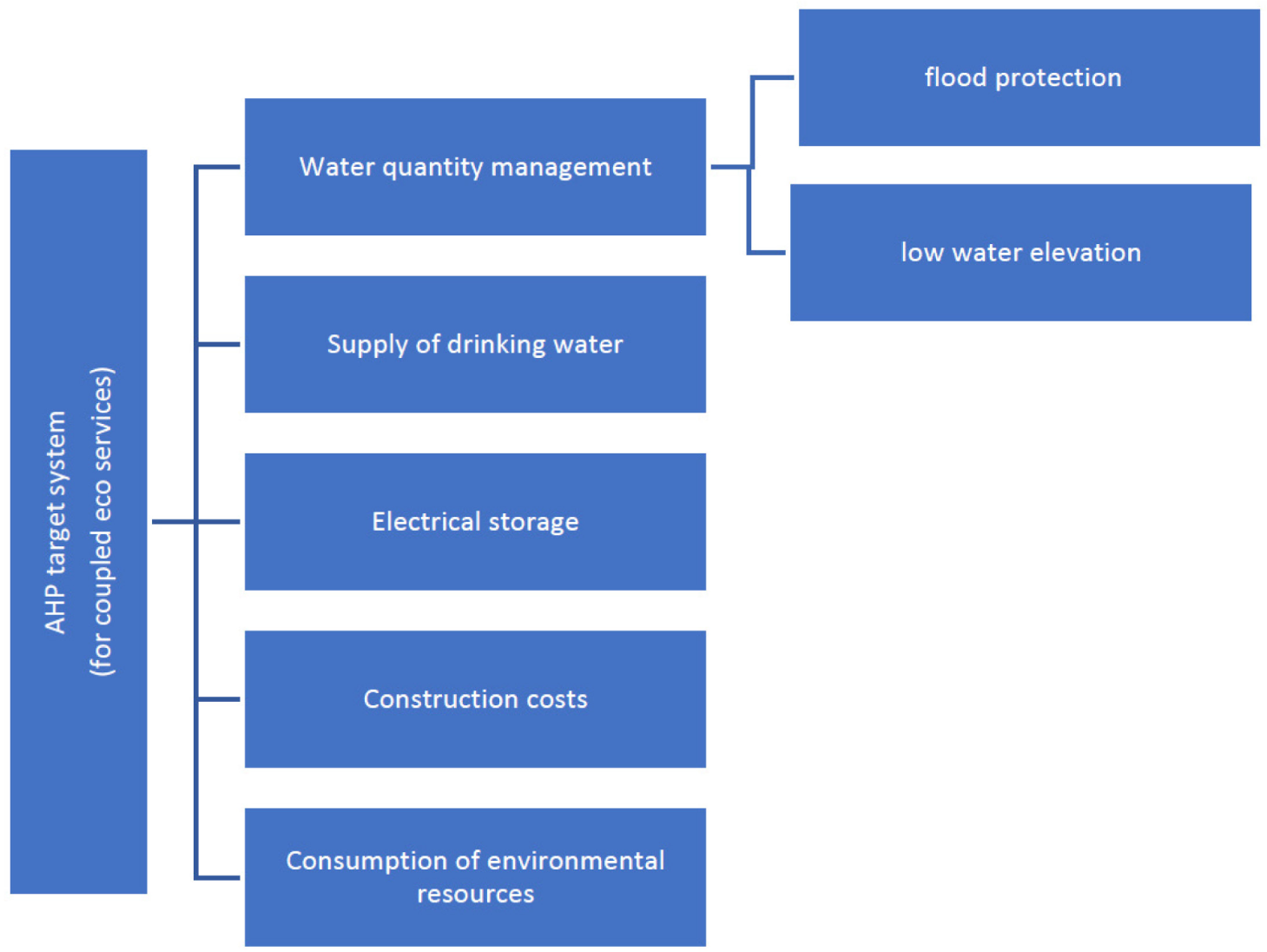
The target system presented in Figure 1 differentiates between two levels. The target dimensions of flood protection and low water elevation were assigned to one common upper dimension, "water volume management". On the same highest level of the target system, the dimensions "drinking water storage" and "electrical storage" were settled as central ecosystem services of the infrastructure project. Since, in addition to the benefits of these ecosystem services, the resource consumption of the respective project should also be an object of the decision-making process and must be taken into account in the assessment, the target dimensions "consumption of environmental resources" (for the interventions in nature associated with the infrastructure measure) and "construction costs" are also located at this highest target level.
The structure of this target system was assigned to the entire project as a task. However, for the evaluation of the alternatives, it is crucial to determine the extent to which the individual target dimensions should be included in the overall assessment. For example, when evaluating a concrete alternative, are the necessary construction costs and the associated consumption of environmental resources more significant than the benefits that arise in the area of drinking water production or electrical storage? As explained above, in the second step, the weights of the individual target dimensions were determined by pairwise comparisons. The approach of the AHP process is not (as with simple variants of scoring models to confront the decision-maker with the simple question of whether they consider a specific target dimension i (e.g., the electrical storage function) to be more important than another target dimension j (e.g., water quantity management) or how many of, e.g., a total of 100 points they would award for the weighting of i and j. Rather, the approach of the AHP is that the decision-makers compare all target dimensions (at the respective level of the target system) with each other. When comparing goal dimensions i and j, the question is not only whetheri is more important than j, but
The application of this method presupposes a series of rationality requirements (axioms) on the part of the decision-makers. It includes, for example, completeness, with which it is assumed that all information required for the evaluation is shown in the target dimensions and alternatives shown on the various hierarchical levels. Also, reciprocity is assumed. Suppose one assumes that a decision-maker is of the opinion that goal dimension iis "much more important" than goal dimension j. In that case, the opinion will also be that feature j is of "much less importance" than feature i. (Elements i and j are therefore to be compared in pairs in such a way that the following applies: aij = 1/aji).
If the AHP is to be carried out as a group process, the individual assessments must be aggregated into a group assessment. Various methods are available for this, such as the arithmetic or the geometric mean, the median value or the modal value of the individual preference expression. In fact, however, only the geometric mean is permissible when aggregating individual values. Only this transformation satisfies the requirement of the transitivity axiom [26], [38], [39]. The individual ratings of the decision-makers m = 1,..., M can be combined to form a common rating as shown in equation (1):
(1)
The aggregation via the geometric mean is permissible both for the weights and for the evaluation of alternatives.
In the third step, the available alternatives are now to be evaluated. Here, too, comparisons of the alternatives should be made in pairs. These pairwise comparisons are to be made within all goal dimensions. Likert scales are also used for this alternative evaluation. However, the preference statement "7" in the comparison of alternatives, for example, now refers to the fact that a certain alternative is rated "significantly better" than another in the respective goal dimension.
The decisive methodological step of the AHP now consists of linking the weights with the alternative evaluations in the respective target dimensions. The combination of weights and evaluation results in the total utility value Φ of each alternative, as shown in eq. (2):
(2)
Where: Φ – utility value, A – alternative, wj – weight of goal j, nij – evaluation of alternative iwith regard to goal dimension j.
A ranking can now be determined from the overall ratings of the alternatives. This ranking corresponds to a rational preference order, which can now be analysed and questioned from several sides. Of course, with a large number of destinations and alternatives and the necessary pair comparisons, there can be inconsistencies in individual preferences. However, the AHP model contains some methods for checking consistency, and it also allows sensitivity analyses with which, for example, the effects of changes in weighting wj on the alternative ranking can be examined.
In the following subsection, the implementation and use of the AHP in the project are explained in more detail, and the ranking of the alternatives presented above is analysed in more detail. Based on the preferences of the individual group members, a collective preference is aggregated. The "objectification" of the decision assumes a well-structured decision problem. However, it does not require somewhat restrictive assumptions about the shape of an individual utility function or a social welfare function. The practical limits of this method are primarily where too many paired comparisons are necessary with many target dimensions and alternatives.
Our project produced two types of results. First, against the background of detailed information about the geological site characteristics and regional estimates of future extreme weather events, the project partners identified a total of 5 project alternatives that are fundamentally able to integrate the various ecosystem services. And secondly, these project alternatives were then subjected to an assessment with the AHP. However, since the descriptions of the alternatives to be evaluated are to be viewed as input from the AHP's perspective, the description of the alternatives is presented in this method chapter. These alternatives differ in terms of the profile of the system services they potentially provide due to their different locations, their geological and ecological site conditions and the infrastructure there. The profile of the respective alternatives was clearly presented in the project profiles, which were presented to the decision-makers during the evaluation process. The essential information about the alternatives can be briefly summarised in the following subsections; a more comprehensive description can be found in the project's final report [12].
At the Okertalsperre (Okertal reservoir), there is a potential upper reservoir located at the soon-to-be-closed quarry on Huneberg-Hill. The Okertalsperre is, therefore, to be partially expanded by the volume of the Huneberg in order to provide more storage capacity for the existing system services at the site in the future. The aim is to create an additional reserve for dry periods and to provide additional retention space for severe flood events. Furthermore, the Huneberg is to be used in combination with the Okertalsperre as a pumped storage plant. The reservoir currently holds 46 million m3, and the empty quarry can hold up to 16 million m3. Of this volume, 2 million m3 will be assigned to the hydropower plant, 2 million m3 will be assigned as a buffer for flooding protection, and 12 million m3 are to be used as a reserve for low water elevation. Since the Okertalsperre is an intermediate storage facility for raw water used for drinking water production, a structural separation within the Okertalsperre would be required in order to protect the main dam body from the direct effects of the pump storage sequences.
Current uses at the location are:
Flood protection
Low water elevation
Generation of drinking water.
This alternative affects the target dimensions:
Improvement of flood protection (reduction of flood volumes by 24%)
Improvement of low water elevation (duration of low water events reduced by 49%)
Slight increase in the supply of drinking water (diversion to the Granetalsperre can be used)
Expansion to include energy storage (to a capacity of 720 MWh and a power of 180 MW, penstock slope ratio† 0.046‡)
Construction costs: €296 million
Consumption of environmental resources: land consumption (water storage areas in the landscape protection area cover 0.26 km2 and in the area of the Huneberg opencast mine 0.43 km2). Spatial resistances in the area of country roads (3.5 km) and hiking trails (0.6 km).
In the Innerstetal (Innerste Valley), there is already a (lower) Innerstetalsperre (Innerste reservoir), which currently serves to protect against flooding, raise low water levels, and obtain drinking water. This location is to be expanded to include the energy storage system service and an above-ground upper reservoir is planned on the Hohestein ridge. At the same time, further storage space is to be created for existing uses in the form of flood protection and raw water storage for drinking water production. For this purpose, the construction of the "upper" Innerstetalsperre is planned between the locations of Wildemann and Lautenthal.
Current uses of the "lower" Innerstetalsperre are:
Flood protection
Low water elevation
Drinking water production.
This alternative aims at the construction of the "upper" Innerstetalsperre and affects the target dimensions as follows:
Flood protection: Expected flood volumes are reduced by 17%
No impact on low-water events
Drinking water supply: additional raw water supply (2.1 hm3/a) through increased transfer to the Granetalsperre
Energy storage with a capacity of 1220 MWh, power of 305 MW, penstock slope ratio 0.14
Construction costs: €268 million
Consumption of environmental resources: use of land in the landscape protection area (0.74 km2 on the upper Innerste; 0.30 km3 in Hohenstein) and spatial resistance in the area of country roads (4 km), loss of cycle path, hiking trail, a war memorial and 4 parcels of land, loss of grassland area (320 m2).
At the Odertalsperre (Odertal reservoir) location, an expansion of the use of drinking water production and energy storage is planned. For this purpose, the site has to be expanded to include an upper reservoir. A structural separation within the Odertalsperre would be required to protect the main dam body from the direct effects of the pump storage sequences.
Current uses are:
Flood protection
Low water elevation.
The measure affects the following dimensions:
No relevance to flood protection
Negative effects on low water levels (due to increased drinking water supply)
Drinking water supply: Significant additional annual raw water supply in the region (9 hm3)
Energy storage: capacity of 1380 MWh and power of 345 MW, penstock slope ratio 0.14
Construction costs: €277 million
Consumption of environmental resources: land consumption due to water storage areas in the landscape protection area (0.095 km2), spatial resistance due to the loss of hiking trails (0.5 km), a monument and green areas (0.36 km2).
In Siebertal (Sieber Valley), various system services can be established at a previously unused and undeveloped location. For this purpose, a dam between the towns of Sieber and Herzberg is planned to be built. An above-ground upper basin for a pumped storage plant can be created on Knollen Hill. The water for drinking water production is to be withdrawn above the town of Sieber at the confluence of the Lonau and Sieber by means of a diversion weir. It can be distributed to the Grane or Sösetalsperre treatment sites.
Current uses: Not existent.
The measure aims at new construction and contributions in the following dimensions:
Flood protection: expected flood volumes will be reduced by 55%
Low water events: Duration of low water events is reduced by 21%
Drinking water production: no impact
Energy storage: capacity of 620 MWh and power of 155 MW, penstock slope ratio 0.14
Construction costs: €208 million
Consumption of environment and nature: land consumption due to water storage areas in the area of a national park (0.8 km2), spatial resistance due to the loss of a country road (3.7 km), cycle paths, hiking trails and an event location, loss of commercial space (1783 m2).
Raising the already existing Grane reservoir dam by up to 15 m primarily serves to ensure drinking water production in the future. The volume of the site can be more than doubled by raising the dam in this way.
Current uses:
Flood protection
Low water elevation
Delivery of drinking water
Power generation.
Increasing the reservoir dam affects the following target dimensions:
Low impact on flood protection (expected flood volumes are reduced by 5%)
No impact on low-water events
Increase in drinking water (additional supply of raw water in the region by 6.6 hm3/a)
No relevance for electricity storage function
Construction costs: €20 million
Consumption of environmental resources: land consumption due to water storage areas and the increase in dam surface in the area of a landscape protection area (1.15 km2), spatial resistance due to the loss of a country road (13 km) and cycling and hiking trails (5 km).
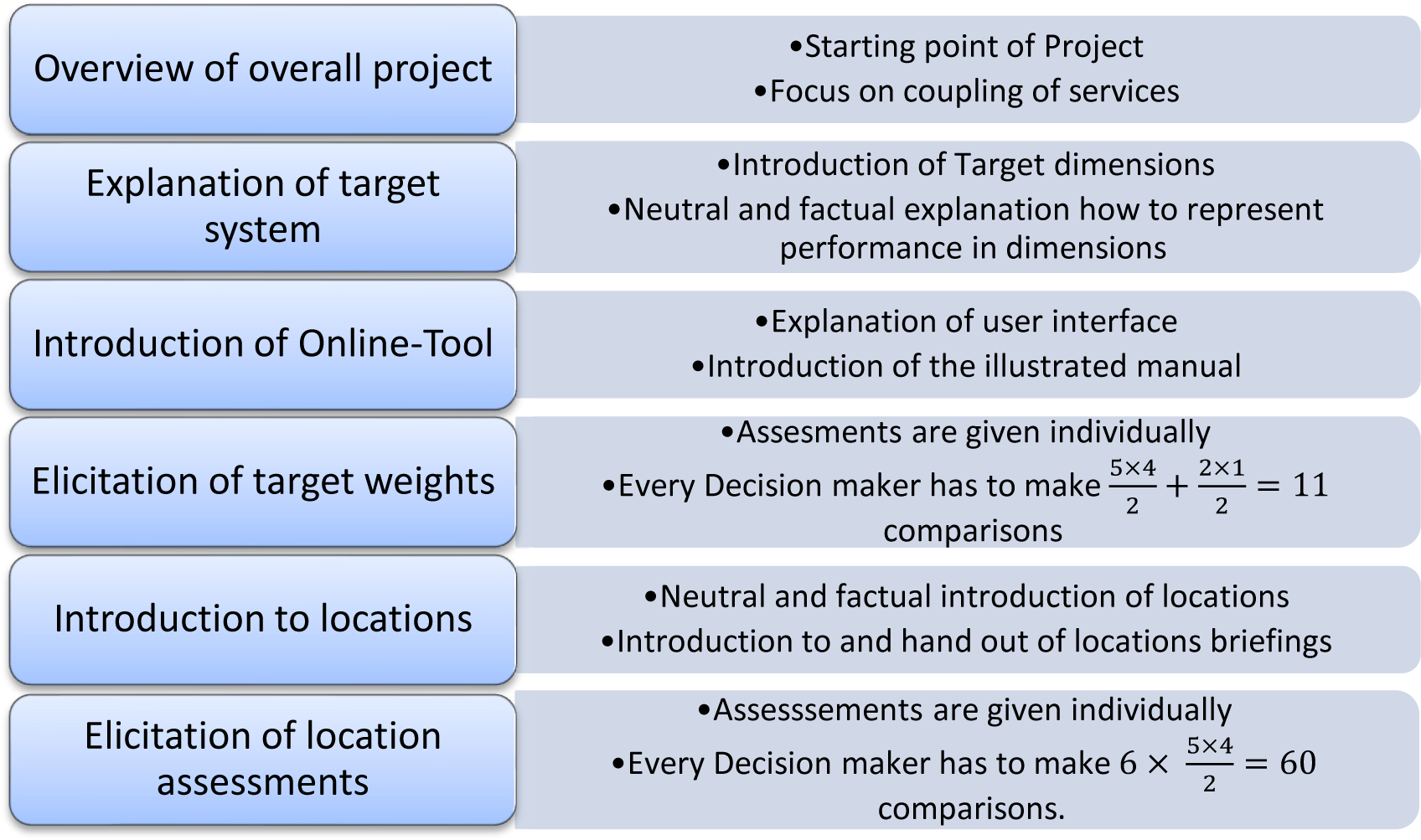
In the Advisory Board meeting on August 31st, 2022, the alternatives presented above were evaluated by ten group members. The project advisory board is a consortium of civil society actors who accompany the project and communicate with the population. Members of the advisory board were energy suppliers, water suppliers, mayors, district administrators, the Lower Saxony State Office for Water Management, Coastal and Nature Conservation, and environmental associations. They accompanied the project from the beginning and thus had the opportunity to get accustomed to the method and the online tool used for the survey in the run-up to the meeting. The tool is the "AHP Online System", which can be accessed via a web browser. It offers the possibility, even in larger groups, to gather target weights and to carry out alternative evaluations. A detailed description of the tool by the developer can be found in Goepel [38]. The data collection session took place in several steps, which are summarised in Figure 2.
Advisory Board meeting for data collection
The results of the evaluation can be summarised as shown in Table 1. The target dimensions are displayed line by line. The global weights of the target dimensions can be found in the "global priority" column. The vector in the underlined font (
Overview of results
| local prio | global prio | Okertal-sperre | Obere Innerste | Odertal-sperre | Siebertal-sperre | Granetal-sperre | ||
|---|---|---|---|---|---|---|---|---|
| Supply, drinking water | - | 0.177 | 0.275 | 0.140 | 0.050 | 0.358 | ||
| Consumption, environmental resources | - | 0.485 | 0.120 | 0.129 | 0.052 | 0.213 | ||
| Construction costs | - | 0.198 | 0.124 | 0.101 | 0.129 | 0.447 | ||
| Electrical storage | - | 0.245 | 0.277 | 0.352 | 0.090 | 0.036 | ||
| Water quantity management | flood protection | 0.756 | 0.418 | 0.251 | 0.059 | 0.180 | 0.092 | |
| low water protection | 0.244 | 0.493 | 0.119 | 0.097 | 0.189 | 0.103 | ||
| Utility | 0.274 | 0.242 | 0.160 | 0.094 | 0.231 |
The weight values in regular font to the right of the column labelled "global prio" are the performance ratings. These values describe how well an alternative is performing within a given dimension. Taking a closer look at the top-most performance rating of 0.177 in line "Supply of drinking water" in column "Okertalsperre": this value is smaller than Grantelsperre's performance rating of 0.358, yet bigger than Siebertalsperre's performance rating of 0.05. Therefore, Okertalsperre provides less utility in the dimension "Supply of drinking water" than Granetalsperre, but it provides more utility within said dimension than Siebertalsperre.
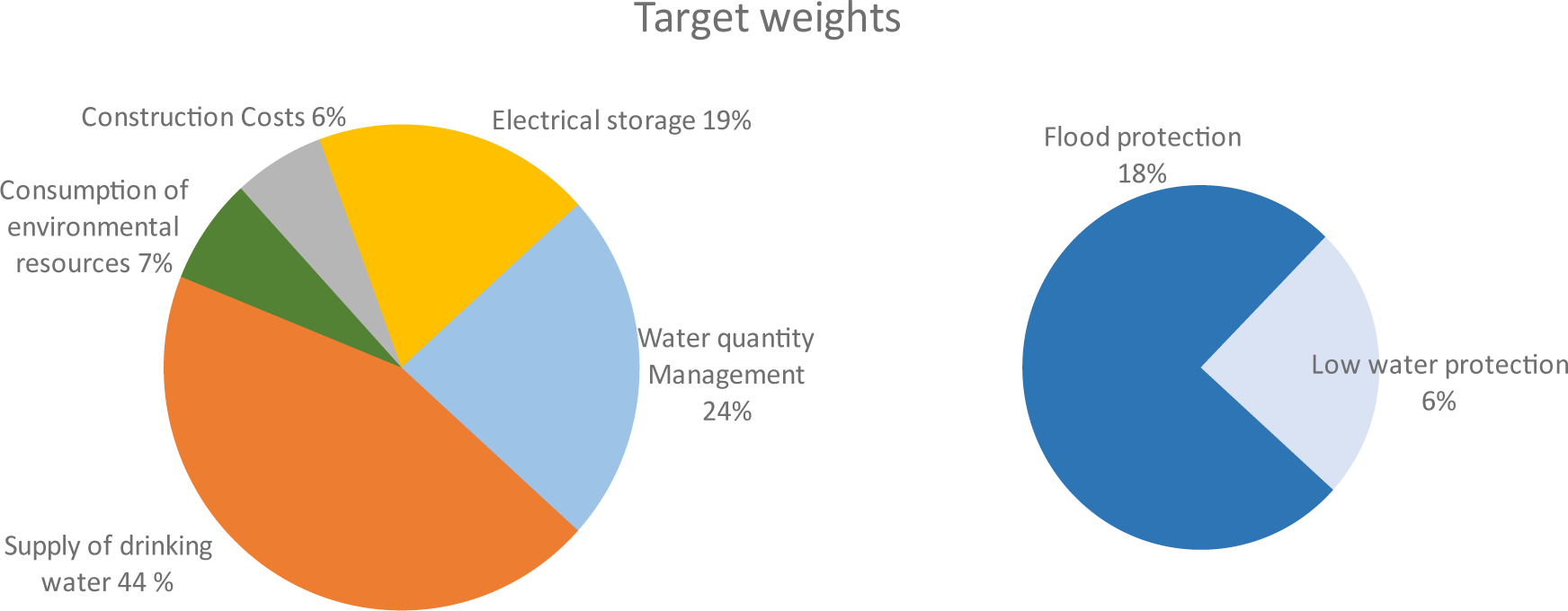
The check of the consistency values (CR is 2.1% = 0.021; not documented here) proves the validity of the results of the preference survey in relation to the weightings of the target system. The assignment of the target weights will be explained in Figure 3, which is a graphical representation of the underlined global priority vector of Table 1. It is noticeable here that the dimension of drinking water is given a very high priority, with 44.5% on the project advisory board. The group members saw the least relevance for the evaluation process in the Consumption of environmental resources.
Target weights
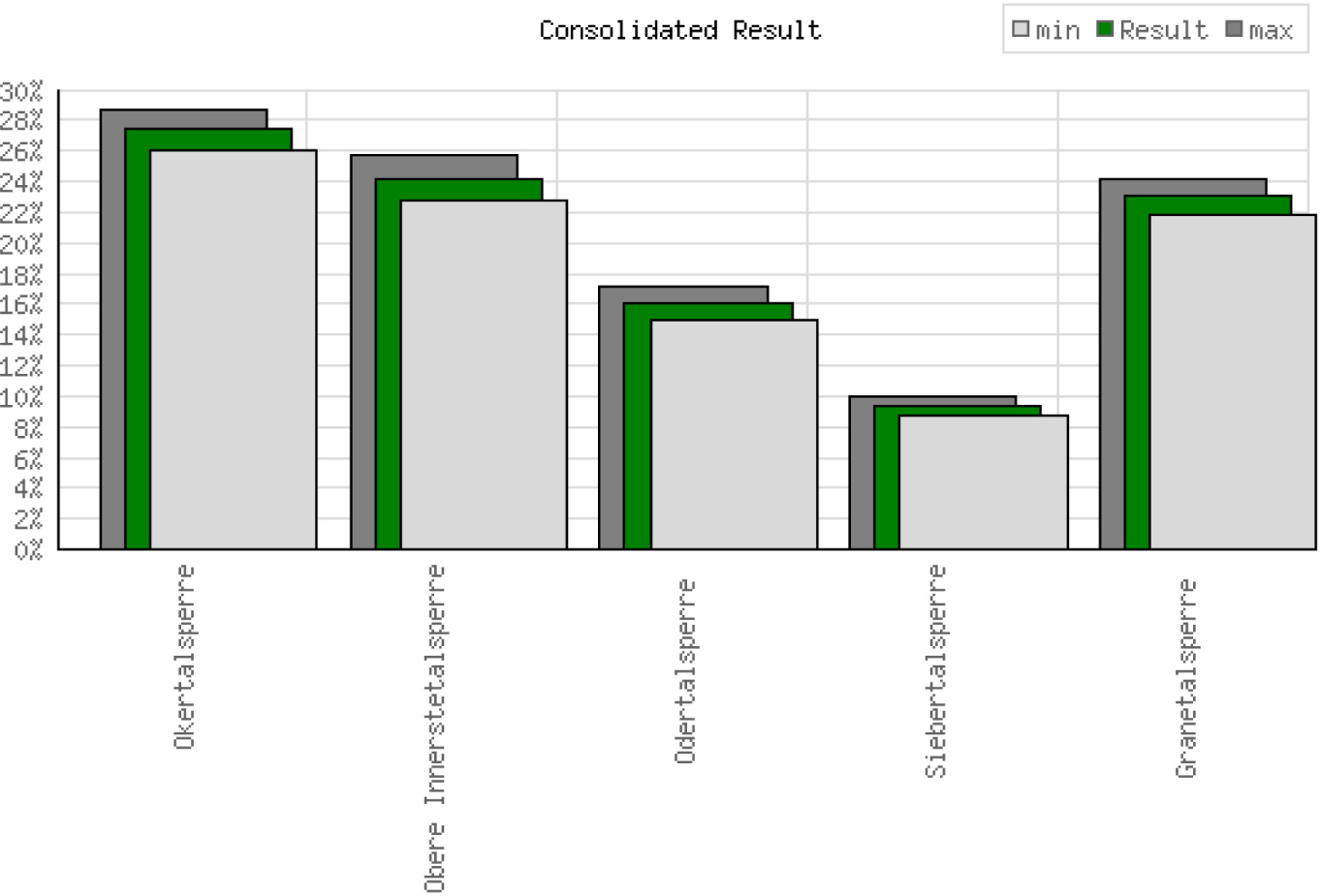
As explained above, target weights and ratings are linked to create utility values that can be found in the bottom row of Table 1. Adding their error bars generates the ranking shown in Figure 4. The main observations from the rating in Figure 4 are the following:
Okertalsperre obviously got the best values in the evaluation.
Although Upper Innerstetalsperre and Granetalsperre receive slightly different aggregated utility values (dark green), the distance between their evaluations is so small that the associated error bars overlap. Therefore, as a result of the decision-making process, both alternatives are to be regarded as equivalent.
Odertalsperre was given third place in this ranking by a relatively large margin.
Siebertalsperre was given fourth place in this ranking by a large margin.
Utility values and error bars; the dark green value is the same as the result in Table 1, and the error bar stretches from light grey (all inconsistencies counted against the alternative - decreasing its utility value) to dark grey (all inconsistencies counted in favour of the alternative - increasing its utility value)
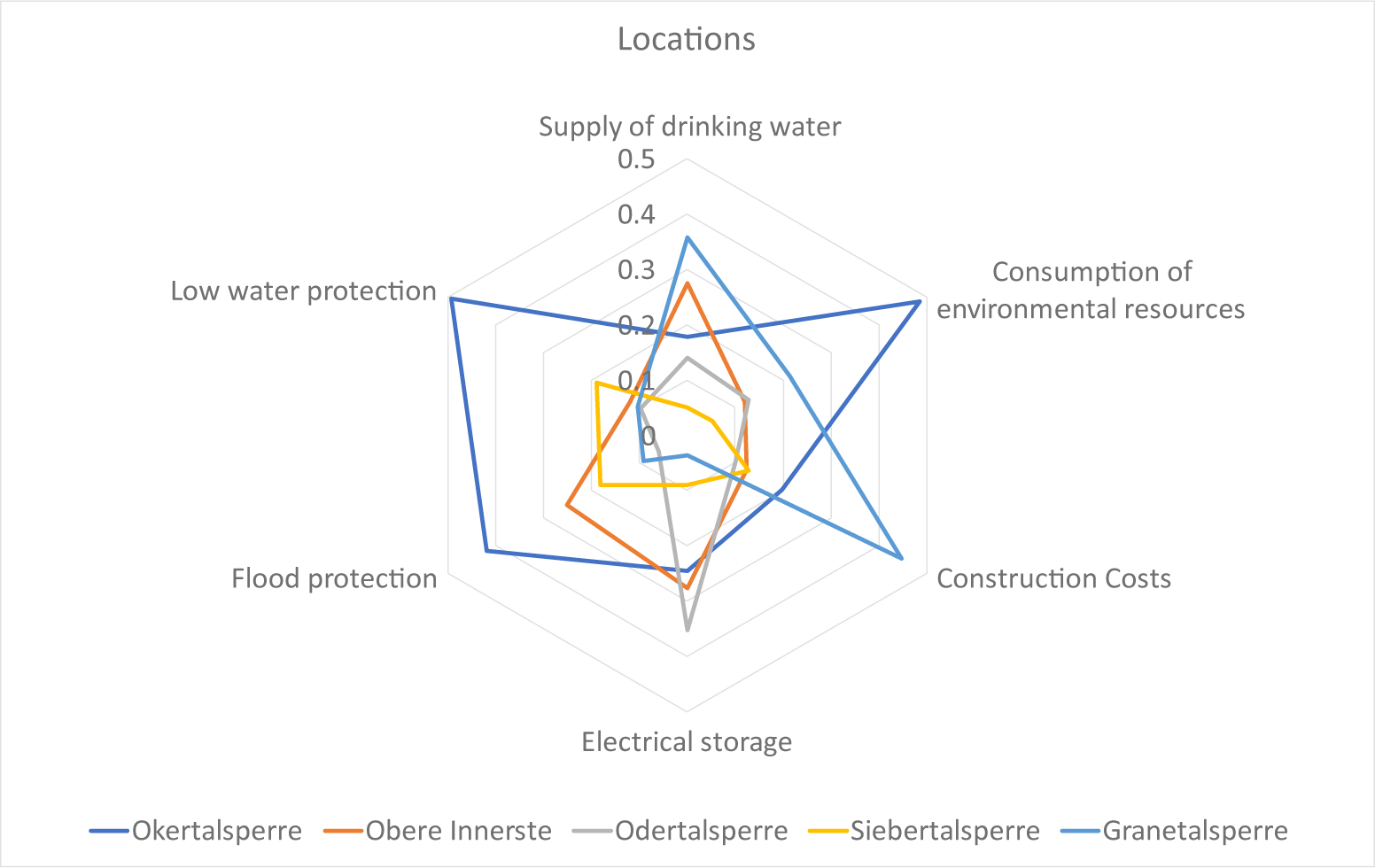
As complementary information on the evaluation results, Figure 5 shows the ratings of alternatives.
Figure 5 shows the performance ratings nij of every alternative i in every target dimension j. While it is the very same data as the performance ratings in Table 1, the spider web diagram nicely illustrates the respective strengths and weaknesses of alternatives within a given target dimension. For example, it becomes clear that the alternative Okertalsperre receives very good ratings in most dimensions compared to the other alternatives. In the dimensions Construction costs and drinking water, the Granetalsperre performs better, but the latter clearly provides less utility than the Okertalsperre in all other dimensions.
Performance ratings of alternatives
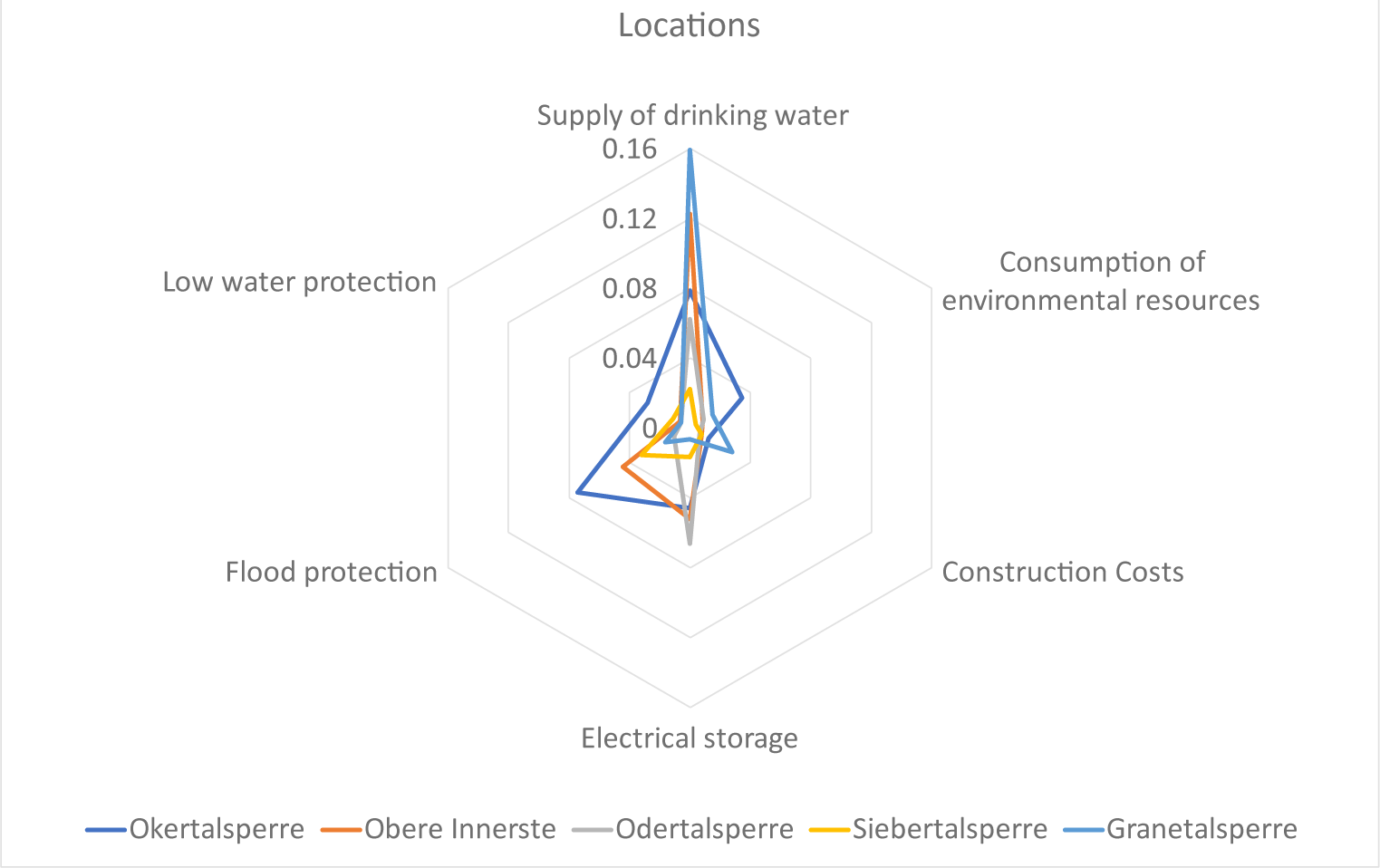
However, by solely using the performance ratings nij, the spider web diagram in Figure 5 does not yet take into account that the target dimensions have different weights wj. While Figure 5 allows us to see the differences within a target dimension, it cannot be used to compare the performance of alternatives between different target dimensions§. This issue is effectively resolved by creating the spider web diagram from the partial utility values (wjnij), as shown in Figure 6. The final utility value Φ(Ai) of an alternative is calculated from the sum of its partial utility values. Therefore, partial utility values plotted in Figure 6 make it possible to compare the size of deflections in different target dimensions with each other.
For example, the peak in light blue (Granetalsperre) in dimension "Supply of drinking water" is calculated by multiplying Granetalsperre's performance rating within the dimension "Supply of drinking water", which is 0.358, with the weight 0.444 of said dimension. All peaks here can now be compared against one another. As a consequence, the figure again points to the great importance of the drinking water dimension for the decision-making behaviour of the group members. Even the second most important target dimension is rated as only half as important. This target weighting and the good result of the alternative Okertalsperre compared to the other alternatives in this heavily weighted dimension, therefore, explains this order of preference.
Partial utility values with respect to target dimensions
The structure and stability of this collective order of preferences over the five alternatives can now be examined using sensitivity analyses. A change in the ranking can result either from a change in the weights or a change in the relative evaluation of alternatives. The critical weighting factor is the weight of a target dimension where the smallest relative change in its value is just enough to change the order of two alternatives. In the present dataset, this critical weight lies in the dimension of electrical storage. The decision-makers gave this dimension a weight of 18.9% in the paired comparisons with the other dimensions. Reducing this weight by 4.4 percentage points down to 14.5% breaks the tie between the Upper Innerstetalsperre and Granetalsperre. In this case, Table 2 shows how Granetalsperre, which does not provide any additional contribution to the target dimension of electrical storage, would clearly be preferred to Upper Innerstetalsperre.
Ranking of alternatives after changing critical weight
| Present ranking | New ranking - changed critical weight |
|---|---|
| 1. Okertalsperre | 1. Okertalsperre |
| 2. Upper Innerstetalsperre ~ Granetalsperre | 2. Granetalsperre |
| 3. Odertalsperre | 3. Upper Innerstetalsperre |
| 4. Siebertalsperre | 4. Odertalsperre |
| 5. Siebertalsperre |
A similar analysis can be conducted when looking into the evaluations of alternatives. The critical evaluation is the evaluation of an alternative where the smallest relative change in its value is just enough to change the order of two alternatives. In the present dataset, this critical evaluation lies in the evaluation of Granetalsperre in the dimension Supply of drinking water. An increase of its evaluation by 2.7 percentage points, to 35.8%, changes the ranking between the Granetalsperre and the Upper Innerstetalsperre, favouring the former, as shown in Table 3.
Ranking after changing the evaluation of alternatives
| Present ranking | New ranking - changed critical evaluation |
|---|---|
| 1. Okertalsperre | 1. Okertalsperre |
| 2. Upper Innerstetalsperre ~ Granetalsperre | 2. Granetalsperre |
| 3. Odertalsperre | 3. Upper Innerstetalsperre |
| 4. Siebertalsperre | 4. Odertalsperre |
| 5. Siebertalsperre |
Since an essential idea of the research project was the simultaneous consideration of different system services from the field of Water quantity management and Electrical storage, it is interesting to examine how strong the weighting of electrical storage would have to be in order to bring about a change in first place in the ranking. The weight of this target dimension would have to be increased from 18.9% to 59.9% in order to remove the Okertalsperre from its current spot atop the rating. Table 4 shows the result of such an increase.
Ranking after increasing the weight of "Electrical storage"
| Present ranking | New ranking - the weight of "Electrical storage" changed to 59.9% |
|---|---|
| 1. Okertalsperre | 1. Upper Innerstetalsperre |
| 2. Upper Innerstetalsperre ~ Granetalsperre | 2. Okertalsperre |
| 3. Odertalsperre | 3. Odertalsperre |
| 4. Siebertalsperre | 4. Granetalsperre |
| 5. Siebertalsperre |
The results presented here are based on an aggregation of a large number of pairwise comparisons that a group of different decision-makers made with regard to the weighting of different target dimensions and the evaluation of alternatives within these target dimensions. The assumptions necessary for this evaluation model aim, on the one hand, at the additive decomposability and completeness of the target system and, on the other hand, require certain cognitive abilities of the decision-makers to make consistent evaluations.
From the individual perspective of a financial investor, the decision-making problem described in this paper is certainly very different than from the perspective of a climate researcher, an environmental organisation, the manager of a waterworks or a public planning and approval authority. In order to balance all these different perspectives on the decision problem, some AHP applications discussed in the literature choose a compromise and only obtain the weighting factors of the target dimensions from preference data. For example, Sun et al. [32], Motiee et al. [33] or Xu et al. [31] use the mathematical interface of the AHP in order to construct a complete and overlap-free target system with precise weightings of the individual dimensions based on expert opinions. However, the concrete evaluation of suitable alternatives is not tied to subjective preference data in these papers; rather, it refers to other information and planning sources, such as geographic information system (GIS) data, life cycle cost data, or technical simulation models. Whether it is possible in this way to identify and implement the best alternatives from the perspective of society is not only a methodological or theoretical question but also linked to political issues, which are beyond the scope of this paper.
In contrast to these approaches, the AHP model in our paper was also applied to the evaluation of alternatives using preference data. In order not to overtax the cognitive capacities of the decision-makers when comparing the alternatives in the respective target dimensions, it was necessary to balance the range of information about the essential properties of the alternatives, also allowing non-experts to make comparisons and evaluations in each respective area. For example, the expected contributions of the alternatives to flood protection or to increasing low water levels in the region were only expressed in percentage figures compared to the current situation. Alternative descriptions of these characteristics, such as data from the insurance industry on avoided flood damage or more complex ecological information on the effects of low water events, might have been interpretable only by certain experts. The same applies, for example, to the presentation and preparation of information on electricity storage options. Since the economic viability of electricity storage depends on the future market prices of electricity and a number of other market developments, the information on electricity storage was provided based on pure capacity figures. In principle, the restriction applies that the evaluation of the alternatives is always tied to the information presented. Decision-oriented evaluation models such as the AHP necessarily differ from more precise financial, engineering or scientific evaluations.
Another aspect to consider when interpreting the results is that current social discussions or recent adverse events might influence the preferences of decision-makers. Certainly, the relatively high weighting of the target dimension of drinking water production has something to do with the dry periods observed in the region in the recent past. In contrast, the relatively low weighting of the target dimension of electrical storage capacity may indicate that the criterion of energy supply security is probably not yet given the importance that experts see in view of the bottlenecks that have not yet been experienced. A further difficulty arises when evaluating project alternatives, such as new dams and dams that would have to be built whole or in part (e.g. Siebertalsperre). Although there are a number of water management arguments in favour of these alternatives, for historical reasons, the support of large parts of the population for such an intervention in landscape areas that have so far been largely economically unused is probably rather low. It cannot be ruled out that this aspect also affects pairwise comparisons that are objectively not affected by this issue. At the same time, it might be that alternatives that could be built on existing capacities (e.g. Okertalsperre) have received a relatively positive assessment against the background of recent flood events in the region.
In summary, however, these aspects do not address a weakness of the AHP. Rather, they reflect actual weightings and discussion processes that shape political decision-making processes and their results in reality. The AHP method used here places particular emphasis on making these weightings transparent.
Climate change creates a growing need for regional adaptation strategies. Part of this adaptation lies in regional infrastructure measures in the area of water management, for example, in the area of flood protection, limiting low water events or drinking water production. However, infrastructure projects, such as the construction or expansion of dams, often face major obstacles. The current situation of hydropower electricity storage is also difficult. Investments in this area are often not economically viable under the current economic conditions for electricity. At the same time, however, the ability to store electricity from renewable energies is an important element for the stability of future energy systems. This project considered five alternative infrastructure projects in the Upper Harz region of Lower Saxony in Germany that would potentially be able to provide coupled ecosystem services in the areas of water management and electrical storage. At the same time, these infrastructure measures could make use of existing above- and underground structures from former mines in the region. In addition to the investment costs, their construction and repair would also require a considerable consumption of natural resources. Given the different profiles of these alternative infrastructure measures, a social decision-making problem arises. How can an evaluation and decision-oriented ranking of conceivable investment alternatives be designed? Due to the innovative nature of the infrastructure measures and the various social, economic and environmental areas affected by them, the application of simple cost-benefit measures or a social welfare function is not possible. There is a problem in determining values because market areas with market prices (such as the electricity industry) and areas of public services (e.g. flood protection) overlap. This social evaluation and decision-making problem cannot be easily optimised using engineering and economic data. Against this background, when evaluating the previously identified infrastructure alternatives with the AHP, a decision-making process was used that is also used in other areas of innovation management in the face of complex multi-dimensional problems. The structure of a target system was, therefore, initially developed with the members of the project advisory board against the background of which the alternatives should be evaluated. This target system became the starting point for two evaluation steps: First, the weights of the target dimensions were determined by the local stakeholders as a democratic group decision. The target weights, which were elicited on an individual basis, were aggregated into consolidated weights. Second, within these target dimensions, the previously explained infrastructure alternatives were evaluated by pairwise comparison. Those evaluations were also aggregated to the group level. In view of the fact that the members of the project advisory board gave the target dimensions of drinking water production a high level of importance, along with their significant emphasis on water volume management (flood protection and low water elevation) and electrical storage, it comes as no surprise that the Okertalsperre was placed first in the ranking. Although it only came in first in "water volume management", it garnered consistently good ratings across all target dimensions. The results of the AHP decision model presented in this paper cannot be generalised in a meaningful way, given the regional characteristics and problems. A greater weighting of construction costs or a greater weighting for electrical energy production would change the ranking. What is generalisable, however, is the structure of the decision-making process. The procedure used here makes the structure of the ranking and the structure of the target system behind it transparent. As long as the weights of the target system and the results of the pairwise comparisons of the alternatives within the respective target dimension are taken as given, the ranking of the alternatives meets the necessary rationality assumptions, for example, with regard to transitivity. The resulting decision is logically coherent and well-justified. Of course, such a decision-making process is not a substitute for the democratic decision-making processes that are necessary in reality and can sometimes be rather complex. However, this procedure, which was used in the project with local stakeholders, is suitable for social participation processes and regional moderation and participation procedures. The AHP, as utilised in this context to facilitate the engagement of local stakeholders, enabled the advisory board to establish their target weights and subsequently evaluate the alternatives based on these weights. This cooperative-participatory process not only circumvented the need to decree trade-offs but, by its inherent nature as a process, fostered substantial civic engagement. In the future, the data generated by the AHP could be employed in discriminant analysis to identify groups of stakeholders with objectively similar or dissimilar interests. In the currently ongoing negotiations to establish a public-private partnership, the results discussed here are being used to bring one of the top-ranking alternatives to light.
This project was a collaborative project of Clausthal University of Technology with several partner universities and industry companies. It was funded by the EU Regional Development Fund (ERDF) Innovation Networks funding line, specialising in the energy industry, with the approval number ZW6-85037489.
- ,
Towards modern sustainable cities: Review of sustainability principles and trends ,J. Clean. Prod. , Vol. 227 ,pp 972–1001 , 2019, https://doi.org/https://doi.org/10.1016/j.jclepro.2019.04.106 - ,
Climate change and mountain water resources: overview and recommendations for research, management and policy ,Hydrol. Earth Syst. Sci. , Vol. 15 (2),pp 471–504 , 2011, https://doi.org/https://doi.org/10.5194/hess-15-471-2011 - ,
Bridging the gap: linking climate-impacts research with adaptation planning and management ,Clim. Change , Vol. 100 (1),pp 87-101 , 2010, https://doi.org/https://doi.org/10.1007/s10584-010-9827-4 - ,
Adaptation action and research in glaciated mountain systems: Are they enough to meet the challenge of climate change? ,Glob. Environ. Change , Vol. 54 ,pp 19–30 , 2019, https://doi.org/https://doi.org/10.1016/j.gloenvcha.2018.10.012 - ,
An Approach to Evaluate Mountain Forest Protection and Management as a Means for Flood Mitigation ,Front. For. Glob. Change , Vol. 5 ,pp 785740 , 2022, https://doi.org/https://doi.org/10.3389/ffgc.2022.785740 - ,
Climate Change Adaptation in European Mountain Systems: A Systematic Mapping of Academic Research ,Mt. Res. Dev. , Vol. 41 (1), 2021, https://doi.org/https://doi.org/10.1659/MRD-JOURNAL-D-20-00033.1 - ,
Scientific Knowledge and Knowledge Needs in Climate Adaptation Policy: A Case Study of Diverse Mountain Regions ,Mt. Res. Dev. , Vol. 36 (3),pp 364 , 2016, https://doi.org/https://doi.org/10.1659/MRD-JOURNAL-D-15-00016.1 - ,
Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range ,J. Hydrol. , Vol. 284 (1–4),pp 244–252 , 2003, https://doi.org/https://doi.org/10.1016/j.jhydrol.2003.08.005 - ,
Projecting Hydroclimatic Extremes: Climate Change Impacts on Drought in a German Low Mountain Range Catchment ,Atmosphere , Vol. 14 (8),pp 1203 , 2023, https://doi.org/https://doi.org/10.3390/atmos14081203 - ,
Technology Overview on Electricity Storage - Overview on the potential and on the deployment perspectives of electricity storage technologies , 2012, https://doi.org/https://doi.org/10.13140/RG.2.1.5191.5925 - ,
Overview of current and future energy storage technologies for electric power applications ,Renew. Sustain. Energy Rev. , Vol. 13 (6–7),pp 1513–1522 , 2009, https://doi.org/https://doi.org/10.1016/j.rser.2008.09.028 - , Energy and water storage Harz - Coupling of sustainable system services for energy storage, flood protection and resource security (EWAZ), (In German, “Energie und Wasserspeicher Harz - Kopplung nachhaltiger Systemdienstleistungen zur Energiespeicherung, zum Hochwasserschutz und zur Ressourcensicherung (EWAZ)),”, 2023
- ,
GIS-based assessment of the opportunities for small-scale pumped hydro energy storage in middle-mountain areas focusing on artificial landscape features ,Energy , Vol. 141 ,pp 1363–1373 , 2017, https://doi.org/https://doi.org/10.1016/j.energy.2017.11.051 - ,
Mine Water for the Generation and Storage of Renewable Energy: A Hybrid Hydro–Wind System ,Int. J. Environ. Res. Public. Health , Vol. 18 (13),pp 6758 , 2021, https://doi.org/https://doi.org/10.3390/ijerph18136758 - ,
Ecosystem Services for Planning Post-Mining Landscapes Using the DPSIR Framework ,Land , Vol. 12 (5),pp 1077 , 2023, https://doi.org/https://doi.org/10.3390/land12051077 - ,
Rethinking Pumped Storage Hydropower in the European Alps: A Call for New Integrated Assessment Tools to Support the Energy Transition ,Mt. Res. Dev. , Vol. 36 (2),pp 222–232 , 2016, https://doi.org/https://doi.org/10.1659/MRD-JOURNAL-D-15-00069.1 - , , Sustainable energy landscapes: designing, planning, and development. in Applied ecology and environmental management, 2013
- ,
Advancing the relationship between renewable energy and ecosystem services for landscape planning and design: A literature review ,Ecosyst. Serv. , Vol. 35 ,pp 241–259 , 2019, https://doi.org/https://doi.org/10.1016/j.ecoser.2018.12.010 - ,
Conflicts between decentralised renewable electricity production and landscape services – A spatially-explicit quantitative assessment for Switzerland ,Renew. Sustain. Energy Rev. , Vol. 67 ,pp 397–407 , 2017, https://doi.org/https://doi.org/10.1016/j.rser.2016.09.045 - ,
From regional environmental planning to implementation: Paths and challenges of integrating ecosystem services ,Ecosyst. Serv. , Vol. 18 ,pp 118–129 , 2016, https://doi.org/https://doi.org/10.1016/j.ecoser.2016.02.031 - ,
Electricity storage systems in the future German energy sector: An optimisation of the German electricity generation system until 2040 considering grid restrictions ,Comput. Oper. Res. , Vol. 66 ,pp 228–240 , 2016, https://doi.org/https://doi.org/10.1016/j.cor.2015.01.014 - ,
The potential of demand-side management in energy-intensive industries for electricity markets in Germany ,Appl. Energy , Vol. 88 (2),pp 432–441 , 2011, https://doi.org/https://doi.org/10.1016/j.apenergy.2010.03.017 - ,
Applicability of multicriteria decision aid to sustainable hydropower ,Appl. Energy , Vol. 101 ,pp 261–267 , 2013, https://doi.org/https://doi.org/10.1016/j.apenergy.2012.05.024 - ,
Development of a multi criteria model for assisting EV user charging decisions ,J. Sustain. Dev. Energy Water Environ. Syst. , Vol. 11 (2),pp 1–23 , 2023, https://doi.org/https://doi.org/10.13044/j.sdewes.d10.0439 - ,
Multicriteria decision making for the choice problem in mining and mineral processing: Applications and trends ,Expert Syst. Appl. , Vol. 121 ,pp 393–417 , 2019, https://doi.org/https://doi.org/10.1016/j.eswa.2018.12.001 - , , Models, methods, concepts & applications of the analytic hierarchy process, 2. ed. in International series in operations research & management science, no. 175, 2012
- , , The analytic hierarchy process: planning, priority setting, resource allocation, 1980
- ,
Group Decision Making with the Analytic Hierarchy Process in Benefit-Risk Assessment: A Tutorial ,Patient - Patient-Centered Outcomes Res. , Vol. 7 (2),pp 129–140 , 2014, https://doi.org/https://doi.org/10.1007/s40271-014-0050-7 - ,
Analytic hierarchy process: An overview of applications ,Eur. J. Oper. Res. , Vol. 169 (1),pp 1–29 , 2006, https://doi.org/https://doi.org/10.1016/j.ejor.2004.04.028 - ,
AHP based multi criteria decision analysis of success factors to enhance decision making in infrastructure construction projects ,Cogent Eng. , Vol. 9 (1),pp 2043996 , 2022, https://doi.org/https://doi.org/10.1080/23311916.2022.2043996 - ,
Benefits of coupled green and grey infrastructure systems: Evidence based on analytic hierarchy process and life cycle costing ,Resour. Conserv. Recycl. , Vol. 151 ,pp 104478 , 2019, https://doi.org/https://doi.org/10.1016/j.resconrec.2019.104478 - ,
An Improved Analytic Hierarchy Process Method for the evaluation of agricultural water management in irrigation districts of north China ,Agric. Water Manag. , Vol. 179 ,pp 324–337 , 2017, https://doi.org/https://doi.org/10.1016/j.agwat.2016.08.002 - ,
A Decision Making Approach for Water Transfer Systems by Analytical Hierarchy Process (AHP) and GIS ,Water Resour. Manag. , Vol. 37 (12),pp 4623–4637 , 2023, https://doi.org/https://doi.org/10.1007/s11269-023-03559-0 - ,
A Review of the Analytical Hierarchy Process (AHP): An Approach to Water Resource Management in Thailand ,Appl. Environ. Res. ,pp 13–32 , 2015, https://doi.org/https://doi.org/10.35762/AER.2015.37.3.2 - ,
AHP-based risk analysis of energy performance contracting projects in Russia ,Energy Policy , Vol. 97 ,pp 559–581 , 2016, https://doi.org/https://doi.org/10.1016/j.enpol.2016.07.024 - ,
The competitiveness of Korea as a developer of hydrogen energy technology: The AHP approach ,Energy Policy , Vol. 36 (4),pp 1284–1291 , 2008, https://doi.org/https://doi.org/10.1016/j.enpol.2007.12.003 - , Developing an AHP based decision model for energy systems policy making, in 2013 IEEE International Conference on Industrial Technology (ICIT 2013): Cape Town, Western Cape, South Africa, 25 - 28 February 2013, IEEE Industrial Electronics Society, Ed., 2013
- ,
Implementation of an Online Software Tool for the Analytic Hierarchy Process (AHP-OS) ,Int. J. Anal. Hierarchy Process , Vol. 10 (3), 2018, https://doi.org/https://doi.org/10.13033/ijahp.v10i3.590 - ,
The Analytic Hierarchy Process (AHP): A method for decision support in healthcare ,(In German, “Der Analytic Hierarchy Process (AHP): Eine Methode zur Entscheidungsunterstützung im Gesundheitswesen”) , Vol. 11 (2),pp 119–132 , 2013, https://doi.org/https://doi.org/10.1007/s40275-014-0011-8




